Traffic calming: a promise unfulfilled

By: Gerald J.S. Wilde

Date: Friday, 29. June 2007

Professor Wilde is the originator of Risk Homeostasis Theory and author of Target Risk 2. He can be reached at the Department of Psychology, Queen's University, Kingston, Ontario, Canada.

Abstract

Archival statistics show marked negative correlation between the annual traffic accident rate per unit distance driven in a jurisdiction on the one hand and the same-year amount of mobility (units of distance driven per head of population) on the other. From 1923 to 1996, the death rate per 100 million miles driven in the U.S. fell on average by between 3% and 4% per annum. In the same period, the mileage per head of population rose on average by between 3% and 4% per annum. The product between these two rates (Acc/Km multiplied by Km/Capita), i.e., the death rate per head of population (Acc/Cap), showed no clear upward or downward trend over the period in question; it was about the same in 1996 as it had been 73 years earlier, in 1923. Major fluctuations in the annual fatal Acc/Cap rate did, however, occur in this three-quarter century and these fluctuations appear to be largely due to variations in the business cycle. Data from several other countries support this notion.

We infer from these observations that interventions that allow drivers to increase their moving speeds-while maintaining both their accident rate per unit time of exposure to risk, and their travel time budget-have an enhancing effect on mobility. These interventions include seatbelts, airbags, wide and forgiving roads, collapsible steering columns and otherwise more crashworthy cars. Conversely, the creation of road conditions, such as "traffic calming" devices (e.g., speed bumps, traffic throttles and chicanes), that compel drivers to slow down, can be expected to decrease mobility while essentially having no effect of the accident rate per capita per year. By the same logic, however, the accident rate per unit distance driven would be expected to rise again. We, therefore, propose that these devices are counterproductive to safety, although they may well have beneficial effects in other respects.

The proposition

The basic proposition of this paper is as follows. To improve safety per unit distance of mobility through traffic engineering technology is to:

1. increase drivers' moving speed
2. to increase mobility per head of population commensurably, and thus
3. to have essentially no effect upon the annual traffic accident rate per capita.

Conversely, to create road conditions, by means of traffic calming devices for instance, that compel drivers to slow down if they wish to maintain the same level of accident risk, is to decrease driver's moving speed, to decrease mobility per head of population and thus once again to have essentially no effect on the annual traffic accident rate per capita. The annual traffic accident rate per capita depends upon the level of accident risk people are willing to accept in return for the benefits they expect from their amount of mobility and the behaviours they display in traffic. Therefore, in order to be effective in reducing the accident rate per head of population, accident countermeasures must effectively reduce the level of traffic accident risk people are willing to accept.

It can be argued that there are predictable relationships from year to year between the following three variables: (1) the accident rate per kilometre driven (Acc/Km), (2) the vehicle kilometrage per head of population (Km/Cap) and (3) the accident rate per head of population (Acc/Cap).

Some of these relationships are trivial of course: (Acc/Km) x (Km/Cap) = Acc/Cap. More interesting is the question why there should be an inverse relationship between Acc/Km and Km/Cap? To put this in another way, why is there is an increase in the total distance driven per head of population as the accident rate per unit distance driven drops?

According to Risk Homeostasis Theory (earlier introduced and sometimes still referred to as "risk compensation theory," Wilde, 1982, 1988, 1994), this phenomenon can be explained as follows. Accident countermeasures that are successful in lowering the rate of Acc/Km are those that allow drivers to proceed at a greater speed without altering their risk of accident per hour of exposure to traffic. The underlying rationale of accident countermeasures in this category appears to be that safety can be enhanced by offering drivers protection from the consequences of risky behaviour, and that this can be done by making the environment more forgiving. We will see below that, paradoxically, there is another category of physical accident countermeasures, the rationale of which appears to be exactly the opposite, namely, that safety can be enhanced by making the consequence of risky behaviour more severe.

Neither category of countermeasures, however, can be expected to alter the level of traffic accident risk accepted by the members of the population. Examples of measures that aim at protecting drivers from the consequences of risky behaviour include the manufacturing of more crashworthy cars, the installation of seatbelts, anti-lock brakes (ABS) and airbags, the widening of roads and the construction of divided motorways. When drivers see no reason to alter their level of accepted risk in the face of these interventions, they will respond to the perceived potential safety benefits of such interventions by travelling at higher speeds and/or by driving more kilometres per year (Km/Cap).

So, if travel time budgets are stable from one time period to another, as has been argued by Zahavi and Ryan (1980), more kilometres will be driven within those time budgets and the per capita safety will not be favourably affected.

It may be inferred from the above reasoning that the provision of greater safety per kilometre driven increases vehicular mobility in two ways: more kilometres per hour of driving and a higher rate of Km/Cap per annum. Therefore, instead of calling these interventions "safety measures," a more appropriate label might be "mobility promotion measures." They have the consequence of increased use of environmental resources but fail to reduce the rate of Acc/Cap. It is conceivable, however, that the increases in both speed and amount of mobility of people and goods make a positive net contribution to the Gross National Product despite the attendant losses (Kamerud, 1988). This issue will not be pursued here, but it has been elsewhere (Wilde, 1994).

An effort was made to find empirical support for the above reasoning. Three approaches were taken:

• analysing time-series data of changes in kilometrage per capita (Km/Cap) in association with changes in the death rate per kilometre driven (Acc/Km);
• analysing cross-sectional data between these two variables, Km/Cap and Acc/Km, within and between jurisdictions; and
• analysing association over time between year-to-year changes in the product of these two variables, i.e., the traffic death rate per capita (Acc/Cap), on the one hand, and changes in the economic juncture (i.e., business cycle) on the other.

Empirical findings: time-series data

Available archival data were inspected on the relationship between a drop in the accident rate per unit distance of mobility (Acc/Km) and an increase in the rate of Km/Cap. Annual Japanese statistics presented by Koshi (1985) were subjected to further analysis. The data indicated that, between 1966 and 1982, the rate of Acc/Km of car and truck travel dropped by an annual average of 11%, and the rate of Km/Cap rose on average by 8% in that period (fatal accidents considered only). The product-moment correlation between the two annual rates was r = -0.97 (Wilde, 1994, p. 136). Thus, the correlation between the two annual rates was close to unity, but the increase in Km/Cap failed to keep pace with the decease in the rate of Acc/Km.

Between 1973 and 1983, the rate of fatal Acc/Km on British motorways dropped by 10% per annum (Department of Transport, 1984). The average year-to-year increase in motorway travel likewise amounted to 10%, while the correlation between the two variables equalled r = -0.88 (Wilde, 1988, p. 458). Precisely the same statistics hold for U.S. interstate highways in the period 1966-1975 (U.S. Department of Transportation, 1977, p. 89; Wilde, 1988, p. 458). Analogous Canadian data between 1955 and 1964 (Whitlock, 1971) show a correlation r = -0.78 between (fatal) Acc/Km driven and nationwide Km/Cap, with a slope of -0.96. Data for Ontario alone in the period 1955-1972 show a correlation r = -0.90 with slope -1.05 (Wilde, 1982, p. 250).

(Figure 1: Traffic death rate per distance travelled, traffic death rate per capita, and the road distance travelled per capita in the U.S., 1923-1996.)

In the U.S., between 1943 and 1972 the correlation between the Acc/Km and the Km/Cap in the aggregate network of roads and streets amounted to r = -0.91 with slope -1.01 (Wilde, 1982b). In 1987 the fatal Acc/Cap rate was about the same as it had been in 1927; in 1996 it was about the same as in 1923. In the course of this 73-year period, the average drop in fatal Acc/Km in each year as compared to the preceding year amounted to 3.24%, while Km/Cap rose about 15% faster, on average by 3.71% relative to the year before. The product-moment correlation between same-year rates of Km/Cap and Acc/Km equals r = -0.89 (while the relationship between Km/Cap and the logarithm of Acc/Km turns out to be stronger still: r = -0.98). The data have been graphed in Figure 1 (which constitutes an update from an earlier graph of statistics up to 1987 by Wilde, 1994, p. 60; data published by the National Safety Council, various years)

The eight cases of (partly overlapping) archival data discussed so far show inverse relationships between the death rate per unit distance driven and the kilometrage per capita amounting to correlation coefficients varying between a minimum of r=-0.78 and a maximum of r = -0.97. The slopes in the eight cases were H" - 0.73 (Japan), H" -1.00, H" -1.00, -0.96, -1.05, -1.01, H -1.00 and +1.15 (U.S.A, 1923-1996) respectively. Most slopes are close to unity, meaning that the increase in the amount of mobility per capita closely matched the decrease in the rate of death per kilometre driven. The Japanese data are marked by a few other oddities as has been pointed out elsewhere (Wilde, 1988, p. 459), while the American data span a very long time period in which other events may have occurred the influence of which we have not been able to identify.

Empirical findings: cross-sectional comparisons

We have seen above that time-series data offer evidence for the notion of an inversely proportional relationship between the accident rate per unit distance driven on the one hand, and the total distance driven per head of population on the other. The question we want to raise now is whether this relationship also holds for cross-sectional comparisons. Again we will refer to archival data, but now pertaining to comparisons within and between jurisdictions at the same point in time.

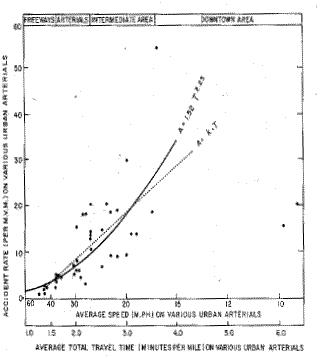
Figure 2: Accident rates per million vehicle miles (m.v.m.) related to average total travel time per mile and moving speeds in various road sections of different road design (graph adapted after May, 1959).

The first is a study by May (1959), who investigated the relationship between the two-year accident history of 40 road and street sections in Detroit and the moving speed of vehicles travelling in these roads and streets. Accident severity was not considered, only accident numbers. For each road section the number of vehicles was counted over a period of 48 hours and the average driving speeds were determined over 84 hours.

From the data plotted in Figure 2 it can be seen that drivers move faster in road sections where the accident rate per kilometre driven (in this case, per million vehicle miles driven) is lower. As can be seen in the graph, May fitted a slightly exponential function to the data, but the data points do not deviate significantly from a linear function A = k.T, meaning that the accident loss (A) equals a constant (k) times the amount of time (T, minutes per mile) spent travelling in each section. This is equivalent to saying that the accident rate per time unit of exposure is essentially the same from one road section to another, and independent of the road geometry, despite its marked differences from downtown streets to expressways. In other words, the rate of Acc/Km varies between road sections, but drivers adjust their speed so that the average Acc/Cap does not change between road sections and remains essentially unaltered across the duration of the trip.

The second cross-sectional comparison involves same-year statistics from 21 different countries published by Borkenstein (1977). Data points from three countries were omitted from analysis because they appeared unrealistic (as they seemed to imply annual driving distances per vehicle of 250,000, 200,000 and 2,000 kms respectively). The correlation between (fatal) Acc/Km and Km/Cap across the remaining 18 countries equalled r = -0.78 with slope -0.924. Thus, in countries where the fatal accident rate per kilometre driven was half as high as in some other country, people drove approximately twice as much.

Macro-economic effects upon the fatal traffic accident rate per capita

Evidence has been offered for the proposition that the rate of Km/Cap is strongly associated with the rate of Acc/Km, in both a time-series as well as a cross-sectional perspective. What has not been discussed so far are the major fluctuations in Acc/Cap from one time period to another in the course of this century. An example of such fluctuation may be seen in Figure 1. The annual traffic death rate ranges from a low of 16.1 per 100,000 residents to a high of 30.8 in the time period considered.

If it is true that these fluctuations are unlikely to be explained on the basis of traffic engineering measures, as we have argued above, then the question of their origin remains to be answered.

Several studies would seem to offer evidence that these fluctuations are the consequence of the business cycle: economic booms are associated with high rates of Acc/Cap in traffic, while economic busts are seen to lead to lower rates of traffic accidents per capita (e.g., Joksch, 1984; Partyka, 1984 and 1991; Wagenaar, 1984; Adams, 1985; Sivak, 1987; Reinfurt, Stewart et al., 1991; Wilde, 1991). One such study (Wilde, 1994) shows the relationship between the per capita death rate on the road in the U.S. and the rate of unemployment as an indicator of the changes in macro-economic prosperity between 1948 and 1987. During this period, 24 of the 39 transitions from one year to the next (1987 minus 1948 equals 39) showed a decrease in the unemployment rate. In 22 of these 24 transitions, there was an increase in the traffic death rate per capita. Over the same time span, 15 transitions from one year to the next showed an increase in the unemployment rate. In 12 of these 15 transitions, there was a reduction in the traffic death rate per inhabitant. The correlation between the employment rate (i.e., the unemployment rate subtracted from 100%) and the same-year death rate per capita amounted to ...

r = 0.66 in the U.S. (1948-1987)
r = 0.69 in Sweden (1962-1987)
r = 0.83 in West Germany (1960-1983)
r = 0.86 in Finland (1965-1983)
r = 0.86 in Canada (1960-1986)
r = 0.88 in the United Kingdom (1960-1985)
r = 0.88 in the Netherlands (1968-1986) and
r = 0.92 in Switzerland (1967-1994).

In the case of Switzerland, the variables involved are somewhat different. As an indicator of the business cycle, we used the number of full-time positions held, aggregated these across all sectors of the economy, and divided their total by the size of the resident population. Instead of annual data, quarterly statistics were used, and instead of simple correlation, an ARIMA time-series analysis was conducted. This resulted in a cross-correlation r = 0.92 between the two variables. When the index of industrial production (IIP) was used as an indicator of the economy, a correlation r = 0.95 was observed on the basis of quarterly data, which are graphed in Figure 3, and r = 0.96 on annual data. The number of jobs held per head of population and the index of industrial production correlated r = 0.87 and r = 0.93 respectively with the total costs of annual insurance claims for property damage due to accidents, this damage being expressed in constant-value Swiss francs (Wilde and Simonet, 1996).

It would seem fair to infer from these multi-national data that the economy has a rather firm influence on the accident rate per head of population. This may be explained in reference to the level of traffic accident risk people are willing to accept. When the economy is in a recession, the benefits expected from risky behaviour are reduced, because time is worth less money. There is less to be gained from driving many kilometres and from driving fast. There is less to be gained from driving through a red or amber light or from cutting corners in other ways. At the same time, the costs expected from risky behaviour are increased, because the costs of accidents, gasoline, car repairs and insurance surcharges for being at fault in an accident, rise relative to real income (Wilde, 1994, p. 67).

There is some evidence that, in periods of economic stagnation, people drive less, while the driving they still do in such periods is performed at a lower accident rate per kilometre driven (Wilde, 1994, p. 76). A more recent analysis of government statistics published by Jacobs (1997, p. 70) shows that the correlation between the differences in the employment rate of all civilian workers in the U.S. between pairs of consecutive years from 1948 to 1995 on the one hand, and the differences in the values of Km/Cap between the same pairs of consecutive years on the other, amounts to r = 0.33, while the correlation with Acc/Km is stronger: r = 0.64. This suggests that, while drops in economic prosperity reduce the amount of driving (or reduce the general year-to-year increase in the amount of driving), they seem to reduce the riskiness of the driving style even more. The implicit this inference here is that changes in the economy cause changes in the quantity and quality of driving, not the other way round.

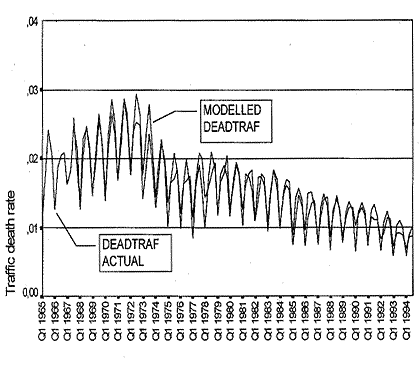
Figure 3: Actual (DEADTRAF ACTUAL) and modelled (MODELLED DEADTRAF, i.e., predicted by the ARIMA procedure) traffic death rate per 100 residents in Switzerland on the basis of the index of industrial production; quarterly data (after Wilde and Simonet, 1996).

The fact that economic factors have a strong influence on the per capita accident rate can also be used to the advantage of safety. In the area of occupational accident prevention, for instance, monetary (as well as other) incentives for accident-free operation have been generally shown the most effective form of accident prevention. Economic incentives have also been successful in promoting safe driving in the general driver population. A discussion of this domain of expertise is beyond the focus of this paper. Individuals interested in these issues are referred to the available literature (e.g., McAfee and Winn, 1989; Wilde, 1994, Chapter 11, and 1998; Geller, 1996).

Ergo, what may be expected from traffic calming measures?

As noted above, there is a paradox between some popular safety policies. This is all the more puzzling as these different safety policies may well be implemented simultaneously and even by the same accident prevention agency. The first policy aims to reduce the severity of the consequences of risky behaviour by the installation of seatbelts, airbags, crash barriers, wide and forgiving roads, collapsible lamp posts, crashworthy vehicles and so forth. The second policy is to increase the severity of the consequences of imprudent behaviour and thus to "scare people into behaving safely." Examples are speed bumps, narrow street passages, barbed wire, rumble strips, pavement undulation, chicanes, speed tables, traffic throttles or pinch points.

Apart from noting that these two policies seem logically contradictory, it has been argued above that neither policy is likely to have an effect on the fatal accident rate per head of population, although they do affect the accident rate per kilometre driven. The first of these (protecting people from the consequences of risky behaviour) causes the accident rate per kilometre driven to diminish, while the second (making the consequences of risky behaviour more severe) can be expected to increase the accident rate per kilometre driven.

As regards the second policy (making the consequences of risky behaviour more severe), one problem in the empirical evaluation of traffic calming measures is located in the possible shift in traffic volume from the treated road sections to other roadways. Accident migration would thus be the result. In a recent paper showing crash reductions due to replacement of traffic signals by multi-way stop signs in Philadelphia, the authors noted: "At this point we can only speculate on the causes of the favourable impact on safety of the signal removals. It is possible, for example, that signal removal was followed by a diversion of traffic to other routes." (Persaud, Hauer et al., 1997). A recent report on the effect of various systems and treatments on drivers' speed had this to say: "It is concluded that traditional methods such as traffic calming can be effective at reducing speeds at isolated sites, However, their effects are localised in time and space, and have the additional drawbacks of lack of public acceptability, secondary costs such as noise and pollution, and possible accident migration." (Comte, V�rhelyi et al., 1997). As a case in point, this report refers to a Norwegian study in which a reduction in car traffic volume by between 33% and 95% occurred as the result of the installation of traffic calming devices in residential areas (Muskaug, 1983). Ironically, such diversion is often one of the stated purposes of traffic calming.

Conclusion

It would seem to follow from the reasoning and data presented here that measures aimed at reducing traffic and rapid traffic flow may be expected to lead to a reduction in the rate of accidents per unit distance of motor vehicle travel (Km/Cap), an increase in the accident rate per kilometre driven (Acc/Km), and no effect on the rate of accidents per head of population (Acc/Cap).

This, however, does not mean that the practice of traffic calming should be abandoned. As traffic safety is not viewed a summum bonum, society may well be inclined to sacrifice a degree of safety for the purpose of obtaining other benefits such as the ones that traffic calming can bring. This has been made patently and painfully clear by the following instance. Dutch authorities prohibited, for the purpose of abating airplane noise in an adjacent residential area, nighttime use of some runways at Schiphol airport in the Netherlands. According to the International Federation of Air Line Pilots Associations, this regulation has seriously compromised safety (Bill, 1998) and it led the federation to extend a "black star" to the airport management (Griffioen, 1998). Some pilots argue that the prohibition has already caused a plane crash in 1997. Traffic calming, indeed.

References

Adams, J.G.U. (1985). Risk and freedom. London: Transport Publishing Projects.

Bill, C. Noise Abatement. Aviation Week, 98.07.15, (http://www.ifalpa.org/if_news/Noise%20Abatement.html)

Borkenstein, R.F. (1977). An overview of the problem of alcohol, drugs and traffic safety. Proceedings of the Seventh International Conference on Alcohol, Drugs and Traffic Safety, Melbourne, Jan. 23-38, pp. 3-11.

Comte, S., V�rhelyi, A. and Santos, J. (1997) Managing Speeds of Traffic on European Roads (The Effects of ATT and Non-ATT Systems and Treatments on Driver Speed Behaviour. Contract No. RO-96-SC.202. Working Paper R 3.1.1. Project funded by the European Commission under the Transport RTD Programme of The 4th Framework Programme.(http://www.vtt.fi/yki/yki6/master/sum311.htm).

Department of Transport, Scottish Development Department, Welsh Office, (1984). Road Accidents Great Britain 1983, London: HSMO.

Geller, E.S. (1996). The psychology of safety. Radnor, Pennsylvania: Chilton Book Company.

Griffioen, P. (1998). Schiphol werkt op rand van veiligheid. [Schiphol operates at the limit of safety]. De Volkskrant, May 15.

Jacobs, E.E. (Ed.) (1997). Handbook of U.S. Labor Statistics: Employment, earnings, Prices, Productivity, and Other labor Data; First Edition. Lanham, Maryland: Bernan Press.

Joksch, H.C. (1984). The relationship between motor vehicle accident deaths and economic activity. Accident Analysis and Prevention, 16, 207-210.

Kamerud, D.B. (1988). Evaluating the new 65 mph speed limit. In J.D. Graham (Ed.), Preventing automobile injury. Dover, Massachusetts: Auburn House, pp. 231-256.

Koshi, M. (1985). Road safety measures in Japan. In L. Evans and R.C. Schwing (Eds.), Human behavior and traffic safety. New York: Plenum, pp. 27-41.

May, A. (1959). A friction concept of traffic flow. Proceedings, 30th Annual Meeting of the Highway Research Board, Washington, D.C., pp. 493-510.

McAfee, R.B. and Winn, A.R . (1989) The use of incentives/feedback to enhance work place safety: A critique of the literature. Journal of Safety Research, 20, 7-19.

Muskaug, R. (1983). Virkninger av gatetun in Oslo og Sandefjord. [Impacts of the living yards in Oslo and Sandefjord]. Oslo: Transport�konomisk Institutt. National Safety Council (various years). Accident Facts. Chicago, Illinois.

Partyka, S.C. (1984). Simple models of fatality trends using employment and population data. Accident Analysis and Prevention, 16, 211- 222.

Partyka, S.C. (1991). Simple models of fatality trends revisited seven years later. Accident Analysis and Prevention, 23, 423-430.

Persaud, B, Hauer, E., Retting, R, Vallurupalli, R. and Mucsi, K. (1979). Crash reductions related to traffic signal removal in Philadelphia. Accident Analysis and Prevention, 29, 803 - 810.

Reinfurt, D.W., Stewart, J.R. and Weaver, N.L. (1991). The economy as a factor in motor vehicle fatalities, suicides and homicides. Accident Analysis and Prevention, 23, 453-462.

Sivak, M. (1987). A 1975 forecast of the 1985 traffic fatality situation: What did we learn form an inaccurate forecast? In J.A. Rothengatter and R.A. de Bruin (Eds.), Road users and traffic safety. Wolfeboro, New Hampshire: van Gorcum.

U.S. Department of Transportation (1977). Highway Statistics Summary to 1975. Washington, D.C.: Government Printing Office.

Wagenaar, A.C. (1984). Effects of macroeconomic conditions on the incidence of motor vehicle accidents. Accident Analysis and Prevention, 16, 191-206.

Whitlock, F.A. (1971). Death on the road: A study in social violence. London: Tavistock Publications.

Wilde, G.J.S. (1982a). The Theory of Risk Homeostasis: Implications for Safety and Health. Risk Analysis, 2, 209-225.

Wilde, G.J.S. (1982b). Critical Issues in Risk Homeostasis Theory: A reply. Risk Analysis, 2, 249-258.

Wilde, G.J.S. (1988). Risk homeostasis theory and traffic accidents: propositions, deductions and discussion of dissension in recent reactions. Ergonomics, 31, 441-468.

Wilde, G.J.S. (1991). Economics and accidents: A commentary. Journal of Applied Behavior Analysis, 24, 81-84.

Wilde, G.J.S. (1994). Target risk: Dealing with the danger of death, disease and damage in everyday decisions. Toronto: PDE Publications.

Wilde, G.J.S. (1998). The concept of target risk and its implications for accident prevention strategies. In A.M. Feyer and A. Williamson (Eds.), Occupational Injury: Risk, Prevention and Intervention. London: Taylor and Francis, pp. 82-105.

Wilde, G.J.S. and Simonet, S.L . (1996). Economic fluctuations and the traffic accident rate in Switzerland: A longitudinal perspective. Berne: Swiss Council for Accident Prevention.

Zahavi, Y. and Ryan, J.M. (1980). Stability of travel components over time. Transportation Research Record, 750, 19-26.

Further comments to this article have been disabled.

---

All Comments (4)

Showing 1 - 4 comments

Leaidan,

Lyuba,

Taylor,

hana bloom,

---